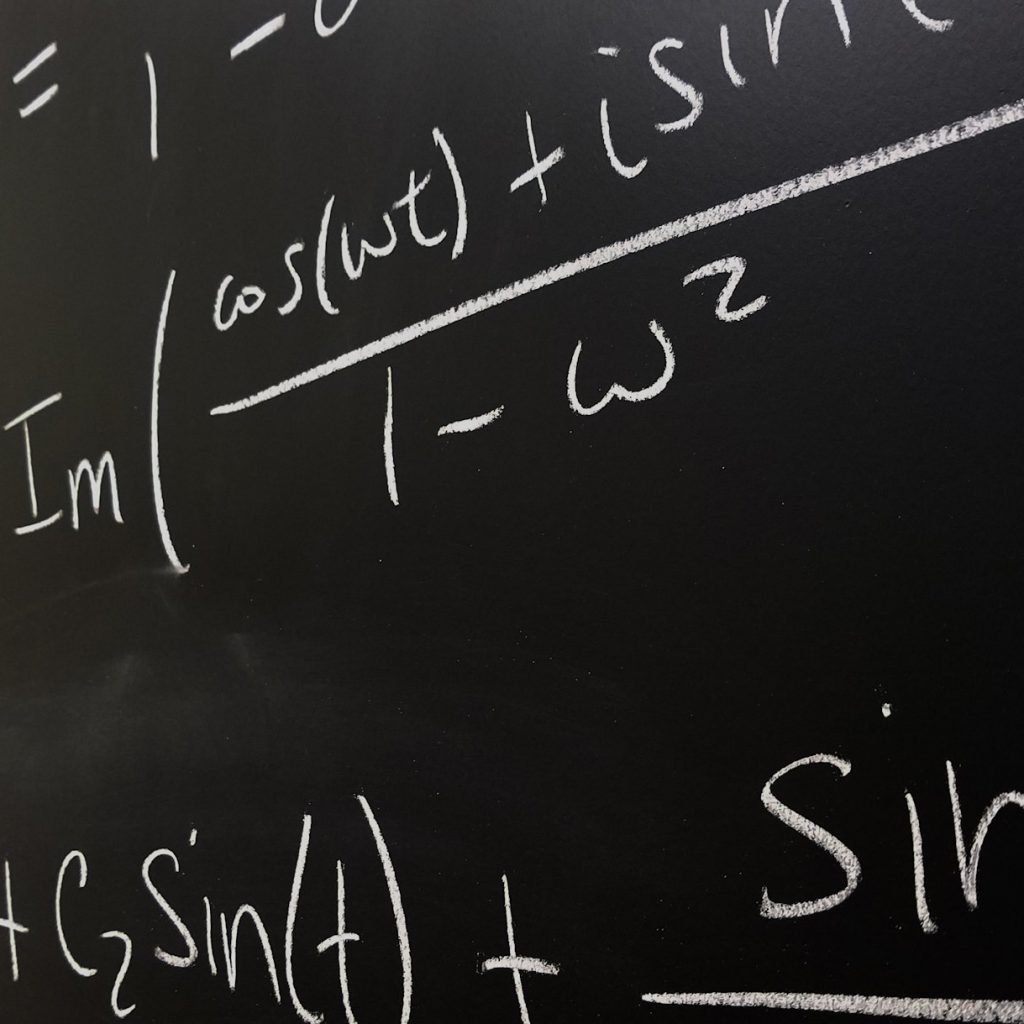هسته ریاضیات مالی

سرفصل دروس ریاضی مالی

مقدمه‌ای بر ریاضیات مالی

بیشتر غیر ریاضیدانان می‌پندارند که ریاضیدانان بااستعداد و باهوش هستند و افرادی کنجکاوند که با جدیت تمام، عمر خود را صرف مسائلی می‌کنند که بسیار مبهم و نامفهوم‌اند. اما در عین حال بر این عقیده‌اند که غیرعملی‌اند و از دور، دستی بر آتش دارند. البته این نوع برداشت از کار ریاضیدانان، صحیح نیست، در طول تاریخ و بیش از همیشه امروز، حوزه‌های اجرایی و عملی بدون کمک و سهم ذهنی آن‌ها با کارایی پیش نرفته و نمی‌رود.

هرچند موقعيت رياضيدانان در دنيای پيشرفته، جا افتاده است، اما چالش پيش روی حرفه رياضي و رياضيدانان کاربردي در ايران تثبيت موقعيت‌های شغلي خود است. در عرصه مالي، البته رياضيدانان ايراني مي‌توانند با ارائه محصول‌های بهتر و جديد، مديريت ريسک بهتر و افزايش سود نهايي شرکت‌ها، هدف‌های کسب وکارها و اقتصاد ملي را تحقق بخشند و موقعيت خود را در عرصه مالي کشور تقويت کنند.

تاریخچه حضور ریاضیدانان در رشته مالی

 با اعطاي جايزه‌ نوبل اقتصاد در سال 1990 ميلادي به سه رياضیدان،چشم‌انداز نويني در مقابل چشمان پژوهش‌گران گشوده شد و عملاً شاخه‌ جديد از علوم متولد شد: نظريه‌ مالي « The theory of finance » تلاش مي‌كند که ساز و كار حاكم بر بازار مالي و چگونگي كار ‌آمد‌تر كردن آن را بررسي و مطالعه كند. اين رشته‌ نو‌ظهور، اصولي را كه بر بازارهای مالي حكم‌ فرماست، توضيح مي‌‌دهد و آن‌ها را روز آمد مي‌كند و در اين راستا بيش از هرچيز از رياضيات بهره مي‌گيرد. تعامل اين دو رشته (رياضيات و نظريه‌ مالي) تا بدان‌جا پيش رفته است كه مسائل مالي اكنون در زمره‌ پژوهش‌های راهبردی در رياضيات است.

ریاضیات مالی

تجزیه و تحلیل اوراق بهادار برای پژوهشگران و تحلیل­گران مالی، اقتصادی، حسابرسان و مدیران ریسک در سازمان­‌های پولی و مالی، از اهمیت بالایی برخوردار است. معمولاَ در تجزیه و تحلیل اوراق بهادار از جمله اوراق قرضه، سهام و اوراق مشتقه بدون داشتن یک مدل ریاضی، اشتباهات ظریف، خطاهای غیر قابل تشخیص و سوءِ تفاهم­‌هایی پیش خواهد آمد که هیچ کدام از گروه­‌های تحلیل­گر مالی و اقتصاددانان نمی‌­توانند و نباید از آن چشم پوشی کنند. خوشبختانه اخیراَ پژوهش­گران و تحلیل­گران مالی و ریسک با استفاده از تکنیک‌­های پیشرفته ریاضی و کمک  ریاضی­دانان و اقتصاددانان توانسته‌­اند مدل­‌های نوینی طراحی کنند که در مقابل تغییرات بازار از خود واکنش نشان داده و برخی از مشکلات بازار را حل کنند. 

رشته ریاضیات مالی علاوه برمطالعه مفاهیم مالی، به تشریح استراتژی مدل­‌سازی بازارهای مالی از جمله بازارهای سهام و مشتقات و روش‌های حل این گونه مدل‌ها می پردازد.  اساتید و دانشجویان در این رشته باید به دنبال مدل‌های ریاضی کمیت‌های مالی از جمله قیمت‌ها، پرتفوی، ریسک، حساسیت‌ها، تغییر پذیری بازار و غیره باشند. محققین این رشته باید دریابند که میان رشته ریاضیات مالی و مدیریت مالی تفاوت‌ها و اشتراکاتی وجود دارد که باید بیشتر به دنبال تفاوت‌ها باشند ، جمله اخیر بدان معنا است که محققین ریاضیات مالی باید به دنبال بررسی موضوعی باشند که آن‌ها را متمایز کند وآن چیزی جز مدل سازی و روش‌های حل پیشرفته ریاضی نیست.

با این توضیح در اين رشته دو رویکرد اساسي وجود دارد:1- معادلات ديفرانسيل جزیی    2-معادلات دیفرانسیل تصادفی
اين دو رویکرد مستقل، هر دو، مجموعه‌ای از تكنيك‌های رياضي هستند كه كاربرد‌های متعددی در سرمايه‌گذاری می‌يابند: ارزش‌گذاری دارايی، مديريت ريسك و مقابله با ريسك، بهينه سازی سهام، مديريت سرمايه‌گذاری در موقعيت‌ها پيچيده‌ اقتصادی و….ازجمله‌ اين كاربردها هستند.

دوره‌ي تحصيلات دانشگاهی مشتمل بر واحدهايي هم‌چون تحليل ريسك بر روی ‌داده‌ها، نرخ بهره، فرايند معاملات ارزی خارجي، عوارض تورم، گزينش حقيقی، تقسيم انرژی، كنترل و بهينه‌سازی تصادفی و ساير مباحث رياضي مربوط به مدل‌سازی مسائل مالی می ‌باشد.
با توجه به نياز فزاينده‌ جوامع به افراد كارآزموده و كلان‌نگر در حوزه‌ها اقتصادی، هم اكنون دانشگاه‌های متعددی در سراسر جهان در اين رشته دانشجو مي‌پذيرند.

معادلات دیفرانسیل جزیی

درمدل‌سازی بازارهای مشتقات به مدل‌هایی می‌رسیم که بر نظریه معادلات دیفرانسیل جزیی استوار هستند. ‌معادلات دیفرانسیل سهموی بیشترین کاربرد را در این زمینه دارند. علاوه بر این در مدل‌سازی نوین با معادلات دیفرانسیلی-انتگرالی و معادلات دیفرانسیل غیر خطی  مواجه می‌شویم. با این توضیح، روش‌های عددی از جمله روش‌های تفاضلات متناهی، کنترل حجمی، عناصر متناهی و این قبیل روش‌ها، کاربرد فراوانی پیدا می‌کنند، زیرا اکثر این مدل‌ها جواب تحلیلی ندارند.

معادلات دیفرانسیل تصادفی

بازارهای سهام معمولا با معادلات دیفرانسیل معمولی و معادلات دیفرانسیل تصادفی مدل‌سازی می‌شوند. بحث در مورد معادلات دیفرانسیل تصادفی نیاز به پیش زمینه قوی فرایندهای تصادفی دارد. در مدل‌سازی نوین با معادلات دیفرانسیل تصادفی مو اجه می‌شویم که در آن‌ها جمله پرش یا رژیم سویچینگ یا تغییرپذیری تصادفی مورد نظر است. در این گونه مسائل نیز جواب تحلیلی یا فرم بسته جواب، قابل محاسبه نیست و تنها روش‌های عددی از جمله روش مونت کارلو روش‌های اویلر، رانگ کوتا و غیره کاربرد دارند.

خواننده باید توجه کند که مسائل متفاوتی در این رشته مورد مطالعه قرار می‌گیرند که در زیر برخی از آن‌ها را بیان می‌کنیم:

برخی مسائل مورد پژوهش در رشته ریاضیات مالی

1. مدل کردن اختیارات به مساله مقدار اولیه و مرزی (معادلات دیفرانسیل جزئی)
2. مدل کردن آتی‌ها به مساله مقدار اولیه و مرزی (معادلات دیفرانسیل جزئی)
3. تخمین تغییر پذیری با استفاده از استراتژی مسائل معکوس
4. تخمین جابحایی(دریفت) با استفاده از استراتژی مسائل معکوس
5. استراتژی منظم سازی
6. مدل‌سازی سبد مالی (معادلات دیفرانسیل تصادفی)
7. مدل‌سازی ریسک  (معادلات دیفرانسیل تصادفی و جزیی)
8. نظریه کنترل بهینه (معادلات دیفرانسیل تصادفی)
9. نظریه کنترل بهینه تصادفی (معادلات دیفرانسیل تصادفی)
10. بهینه‌سازی سبد مالی (معادلات دیفرانسیل تصادفی)
11. روش‌های حل معادلات دیفرانسیل جزیی-تحلیلی و عددی
12. روش‌های حل معادلات دیفرانسیل تصادفی-تحلیلی و عددی
13. روش‌های حل معادلات دیفرانسیل معمولی-تحلیلی و عددی
14. روش‌های حل مساله کنترل بهینه (تصادفی-تعینی)-تحلیلی و عددی
15. ریسک بازار، مدل‌سازی و روش‌های حل

فرصت‌های شغلی ریاضیدانان مالی

رياضيدانان در گذشته به غير از تدريس، از طريق مدل‌سازی اقتصادی صنعتی وارد کسب وکارها می‌شدند: به عنوان مثال، طراحي بال هواپيما را انجام مي‌دادند، تأثير مواد منفجره در معادن را محاسبه مي‌کردند و طراحي بهينه تيغ ريش تراش را عهده دار مي شدند. اکنون حوزه مالي پتانسيل بيشتری براي جذب رياضيدانان از ساير فعاليت‌هاي اقتصادی از خود نشان می‌دهد.در دنيای امروز، فرصت‌های شغلي پيش روی رياضيدانان به تدريس يا مدل سازی رياضي صنعتي محدود نيست،  بلکه حوزه فعالیت رياضيدانان بسیار وسیع شده که در اینجا در نظر داریم برخی از فرصت‌های شغلی محققین ریاضیات مالی را به اختصار معرفی کنیم:

برخی فرصت‌های شغلی رشته ریاضیات مالی

1. شرکت‌های بیمه
2. سازمان بورس و اوراق بهادار
3. شرکت‌های سرمایه گذاری
4. بانک‌های سرمایه گذاری
5. بانک‌های تجاری
6. شرکت نفت آتی‌های نفت بخش فروش
7. بورس فلزات
8. شركت‌های خزانه‌داری